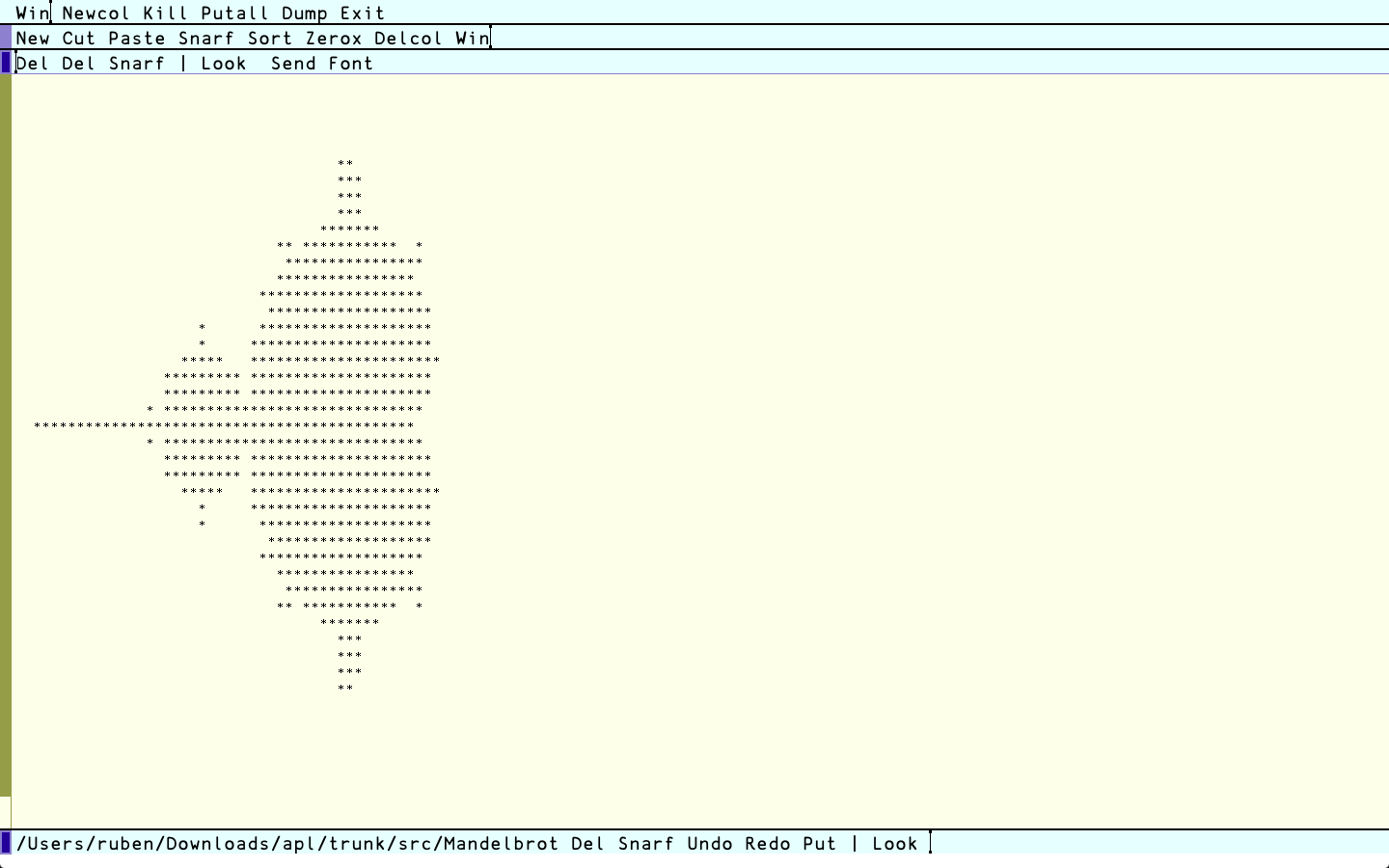
The Mandelbrot set in one line of APL
8 minutes read | 1519 words by Ruben BerenguelIs this line noise?
⍉' *'[⍎'1+0<|z',(∊150⍴⊂'←c+m×m'),'←c←(¯2.1J¯1.3+(((2.6÷b-1)×(¯1+⍳b))∘.+(0J1×(2.6÷b-1)×(¯1+⍳b←51))))']
Nope. This is not line noise, but a complete APL program to display the Mandelbrot set in glorious ASCII, with asterisks and spaces just like Brooks and Matelski did a long time ago while studying Kleinian groups (it’s a short paper, read it someday). I’ll explain in (a lot, I hope) detail this line in a few moments. So, what’s APL first?
APL is literally A Programming Language. Funny, isn’t it? Its origins can be traced back to a way to formalise algorithms created by Kenneth Iverson while at Harvard. It is famed as a very cryptic language, for a reason. Its fundamental functions are unicode chars, and at first it feels extremely weird.
I got interested in it after finding an iOS interpreter for J, a programming language developed as a successor to APL, also by K.I. It just got away without Unicode, leaving only cryptic dygraphs, like <.@o. (from a Wikipedia example of high precision computing.) J is very cool, in that it offers a terse syntax to operate with matrices and vectors, very much like Matlab (Octave in my case) or R. But I felt I’d rather check the first idea, before diving into the even weirder syntax of J. So, it was APL.
The first problem was finding a good APL interpreter. Most were paid (and extremely expensive) and I could only find 2 APL interpreters working in Mac OS. One is NGN APL an implementation focused on node.js Also usable on a browser, so it is cool. But I’d rather get a little closer to the system… And decided to use Gnu APL instead. Of course, using an emacs mode for gnu-apl. Caveat: make sure to add
export LC_ALL=es_ES.UTF-8
export LANG=es_ES.UTF-8
to your .zshrc or similar, without it you’ll need to add a hook to gnu-apl mode reading
(set-buffer-process-coding-system 'utf-8 'utf-8)
to make sure emacs and apl talk in utf-8. Without it, there are no commands to send to the interpreter!
Since I’m also a heavy acme user, and acme is well-known in its unicode support, I used it instead to develop that line above. But emacs works correctly, I just like having things to tinker with acme.
Getting back to the line-noisiness of APL, first you need to know that precedence is right-to-left, so
3×3+1
in APL yields 12 instead of the expected 10. You can change this with parentheses. Now that I have taken this out, we can analyse the line above. Instead of explaining it from right to left, I’ll explain how I proceeded to develop it.
Iterating the quadratic polynomial
(∊150⍴⊂'←c+m×m')
Succintly (I could explain a lot of the mathematics behind, but I just want to do a picture today) to draw the Mandelbrot set we need to find complex points c=x+iy (remember: you can think of a complex point as a point in a plane, like a screen: it has an x coordinate and a y coordinate) such that computing
$$f(z)=z^2+c$$
a lot of times with z=c is eventually a point outside a circle of radius 2. For instance, if c=1 this would be:
- $$f(1)=1^2+1=2$$
- $$f(f(1))=f(2)=2^2+1=5$$
- $$f(f(f(1)))=f(5)=25+1=26$$
And so on. In this particular case, after the first iterate we could stop. Remember that to do so, the product c·c is the product of complex numbers.
So the first part I wanted to get out of my way was generating this iteration. There are several ways to do it in APL, but a very cool way I found was to first generate the required computation like above. How?
'c+m×m'
computes exactly this, if m=c or if m is any other iterate, like m=f(f(f(c))). In APL speak, making m hold the same as c would be
m←c
and with right-to-left priority,
c+m×m←c
means “assign to m the value of c, multiply m by m (remember: it’s the same as c) and add c.” Likewise,
c+m×m←c+m×m←c
ends is computing the 2nd term in the list above, if c is 1. So we have a pretty clear idea of how it should look like:
something←c+m×m←c+m×m←c+m×m←c+m×m←c+m×m←c+m×m←c+m×m←c
This is essentially “many times” the string c+m×m. There’s a very, very easy way to repeat something in APL. For instance, 3 ⍴ 1 (read 3 reshape 1) creates a vector with three ones, 1 1 1. Reshape essentially multiplies or trims vectors. But… 3 ⍴ 'tomato' is ‘tom’. The reshaping also cuts, of course! What we need is to make APL treat the string c+m×m as one element. This is done with the next instruction in the Mandelbrot line, as you may guess: encapsulate.
⊂'←c+m×m'
ensures APL treats it as one element, so
20⍴⊂'←c+m×m'
generates a neat and long string of what the iterates should look like. To make sure the final string makes APL-sense, first we enlist with ∊: turns the vector of repeated iterates into just one iterated element, like a long string all together. This could actually be removed, but it allowed me to learn a new function and I think it’s pretty interesting. To end in a proper way, we add to the string a receiver variable z and fuse the strings with ,.
I know this was long, but the iteration was the trickiest part!
Generating the grid of points
'←c←(¯2.1J¯1.3+(((2.6÷b-1)×(¯1+⍳b))∘.+(0J1×(2.6÷b-1)×(¯1+⍳b←51))))'
Since APL is cool with matrices (and complex numbers!) we can assign to the initial c a whole matrix of complex points (our screen pixels) and then we’ll have all the data required for the picture.
This weird piece is just a compact way of generating a grid. To make it easier to understand,
⍳5
(that’s read as iota 10) generates the sequence 1 2 3 4 5. To create a matrix we need two sequences (one for the $x$ coordinates and another for the $y$ coordinates.) For the complex numbers we can do
0J1 ⍳× 5
which yields 0J1 0J2 0J3 0J4 0J5. As you may guess if you’ve been following, 0J1 is just the complex number $i$. For some weird reason APL uses the j letter instead of $i$. No big issue. Now we have the $x$’s which go from 1 to 5 and the $y$’s which go from $i$ to $5i$. Whichare then all the complex points in the plane we are creating? This means adding one of each $x$ to each $y$, to get a grid. Similar to a multiplication table, but with sums instead of products. APL magic to the rescue, there is a function for that’s
(⍳5) .+ (0J1×(⍳5))
returns
1J1 1J2 1J3 1J4 1J5
2J1 2J2 2J3 2J4 2J5
3J1 3J2 3J3 3J4 3J5
4J1 4J2 4J3 4J4 4J5
5J1 5J2 5J3 5J4 5J5
which is pretty close to what we need. To plot the Mandelbrot set we are only interested (mostly, and in this particular instance) in points with real coordinate $-2.1<x<0.5$ and complex coordinate $-1.3<y<1.3$ (just to make it square which is easier to reason). So, the next long APL blurb just adds a matrix similar to the one above to a complex point, generating the grid of points we want, and assigns it to c. Almost done!
Computing and plotting
⍉' *'[⍎'1+0<|z',
After we have the set of points in c, we merge this string (with comma) to the iteration we developed above. At the far right of the iteration we find this piece:
'1+0<|z',
As you may guess, this adds to the string we have constructed the term 1+0<|z which from right to left does:
- Compute the norm (distance to the origin) of the final iterate, which was assigned to
zat the end of the iteration, the norm is computed with| - Check if this is larger than 4. This generates a matrix of 1s and 0s (for booleans)
- Add 1 to all entries of this matrix (so we have a matrix full of 1s and 2s
Note: The first version of this code had 0<|z, which works well for rough images of the Mandelbrot set, since most iterates are eventually INFNAN, which is a funny number in programming, since it is positive, smaller than 0, different from itself, etc. This is cleaner though.
We have a neat string which can generate a matrix of 1s and 2s and represent the Mandelbrot set. How do we make this string compute something? Meta-magic
⍎
(known as execute) takes a string and computes it as an APL function. Just like eval in Lisp, Javascript or Python.
Represent it neatly
⍉' *'[stuff]
Since a matrix can be used to index a vector, we use this newly computed matrix as indexes (i.e. between square bracket) with the vector ' \*' so we get almost a Mandelbrot set. But since I was slightly lazy when generating the grid of points, it is transposed. ⍉ (transpose) fixes it and finishes the line and the program.
Conclusion
Writing this line of code took me quite a long time, mostly because I was getting used to APL and I didn’t know my way around the language. Now that I’m done I’m quite impressed, and I’m looking forward to doing some more fun stuff with it. And if possible, some useful stuff.